以梯度下降法解線性迴歸係數
程式說明
此篇文章說明如何用梯度下降(Gradient Descent)方法找出線性迴歸最佳參數解。實作參考自國立台灣大學資訊網路與多媒體研究所李宏毅老師的Youtube教學影片:
使用套件
tidyverse為R軟體專為資料科學的集合套件,裡面包含常用的dplyr及ggplot2等常用的資料科學套件。詳情資訊可至tidyverse套件官網查看。
library(tidyverse)使用資料集及分析問題
本次資料集使用ggplot2套件內提供的鑽石(diamonds)資料集,裡面共包含53,940筆及10個特徵資料。分析的問題為給定在切割(cut)為理想型(Ideal)及淨度(clarity)為內部完美無瑕(IF)的鑽石資料集下,以克拉做為特徵資料(即解釋變數),建立線性迴歸模型,預測鑽石價格(即被解釋變數)。有關鑽石的知識,可參考此網站。
預測的迴歸式如下,下標i代表樣本:
\[Price_i=\hat{\alpha} + \hat{\beta_1} Carat_i + \varepsilon_i\]
資料整理程式碼如下所示:
data <- diamonds %>%
filter((cut=="Ideal") & (clarity=="IF")) %>%
select(price, carat)
data## # A tibble: 1,212 x 2
## price carat
## <int> <dbl>
## 1 2783 0.52
## 2 2789 0.55
## 3 2790 0.64
## 4 2800 0.61
## 5 2802 0.53
## 6 2868 0.62
## 7 2869 0.62
## 8 2925 0.71
## 9 2952 0.74
## 10 2960 0.64
## # ... with 1,202 more rows經過filter挑選切割(cut)為理想型(Ideal)及淨度(clarity)為內部完美無瑕(IF)的鑽石資料集後,只剩下1,212筆資料。
迴歸函數與封閉解法
我們直接透過R軟體的lm函數,直接跑線性迴歸模型,估計出參數值。
model <- lm(price ~ carat, data = data)
model##
## Call:
## lm(formula = price ~ carat, data = data)
##
## Coefficients:
## (Intercept) carat
## -3043 11682估計出來的模型的\(\hat{\alpha}=-3403\),\(\hat{\beta_1}=11682\)。
繪製圖形觀看迴歸線配適狀況:
ggplot(data, aes(x = carat, y = price)) +
geom_point() +
stat_smooth(method = "lm")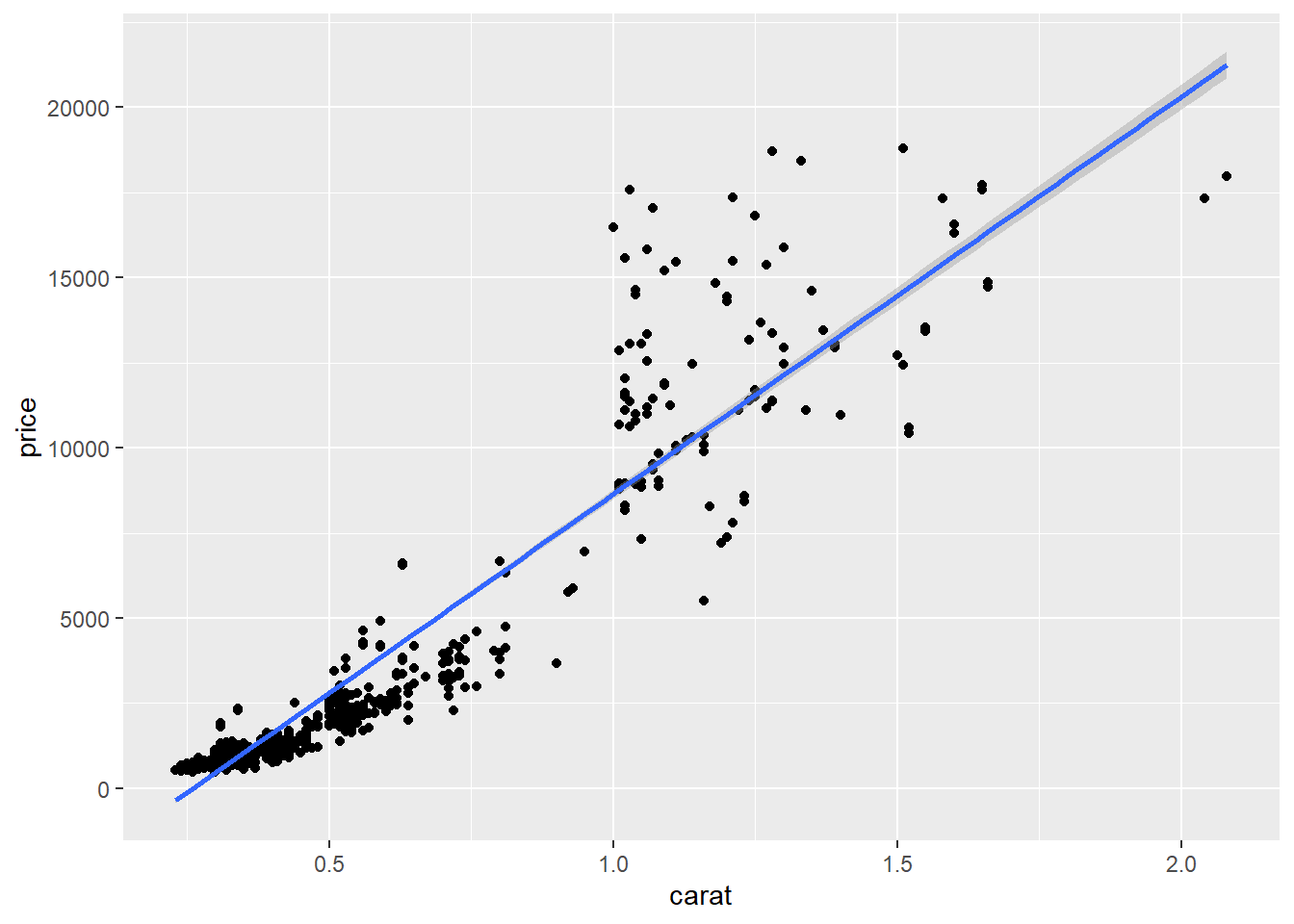
除透過程式的函數外,也可直接以線性迴歸的封閉解(Closed-form solution)進行計算:
\[\beta=(X^TX)^{-1}X^TY\]
# 整理解釋變數資料並轉為matrix格式
x <- data %>%
transmute(Intercept = 1, carat) %>%
as.matrix()
# 整理被解釋變數資料並轉為vector格式
y <- data %>% pull(price)
# 封閉解
beta <- (solve(t(x) %*% x) %*% t(x) %*% y)
beta## [,1]
## Intercept -3042.77
## carat 11681.76可以發現封閉解解法和套件執行的結果是一樣的。
梯度下降法
為了有「機器學習」的感覺,此處示範以梯度下降法的方式,來找出線性迴歸最佳的參數。
在線性迴歸模型中,誤差函數(Error Function)為均方誤差(MSE, Mean squared error):
\[ L(\hat{\alpha}, \hat{\beta_1}) = \frac{1}{N} \sum_{n=1}^{N} (y_{i}-\hat{y_{i})}^{2}=\frac{1}{N} \sum_{n=1}^{N}(y_{i} - \hat{\alpha} - \hat{\beta_1} Carat_i)^{2}\]
接下來將誤差函數對\(\hat{\alpha}\)及\(\hat{\beta_1}\)進行偏微分,得到梯度下降的計算式:
\[\frac{\partial L}{\partial \hat{\alpha}} = \frac{1}{N} \sum_{n=1}^{N} 2(y_{i} - \hat{\alpha} - \hat{\beta_1} Carat_i)(-1)\]
\[\frac{\partial L}{\partial \hat{\beta_1}} = \frac{1}{N} \sum_{n=1}^{N} 2(y_{i} - \hat{\alpha} - \hat{\beta_1} Carat_i)(-Carat_i)\]
每次疊代時,參數依據學習比率乘上梯度值進行調整。
# 設定梯度下降參數
lr <- 0.1 # 學習比率
maxIterations <- 20000 # 最大疊代次數
y <- data$price # 被解釋變數資料
x <- data$carat # 解釋變數資料
alpha <- 0 # 截距項初始值
beta <- 0 # 解釋變數係數初始值
iterations <- 1 # 疊代次數起始值
traningRecord <- tibble(alpha, beta) # 儲存訓練過程資訊
while(iterations <= maxIterations){
# 以目前的截距項及特徵係數值進行預測
yPred <- alpha + beta * x
# 損失函數對截距項進行偏微分
alphaGrad <- sum(2 * (y - yPred) * (-1)) / nrow(data)
# 損失函數對特徵係數進行偏微分
betaGrad <- sum(2 * (y - yPred) * (-x)) / nrow(data)
# 提前終止條件
if((abs(alphaGrad)<=(10^(-5))) & all(abs(betaGrad)<=(10^(-5)))){
cat("在第" ,iterations,"次 疊代已達收斂條件\n")
break
}else if((abs(alphaGrad)>=(10^(10))) & all(abs(betaGrad)>=(10^(10)))){
cat("在第" ,iterations,"次 確認數值發散,終止運作\n")
break
}
# 調整截距項及特徵係數值
alpha <- alpha - lr * alphaGrad
beta <- beta - lr * betaGrad
# 記錄疊代次數
iterations <- iterations + 1
# 記錄訓練資訊
traningRecord <- traningRecord %>%
bind_rows(tibble(alpha, beta))
}## 在第 1582 次 疊代已達收斂條件# 整理學習結果
tibble(Intercept = alpha, carat = beta)## # A tibble: 1 x 2
## Intercept carat
## <dbl> <dbl>
## 1 -3043. 11682.由結果可以看出,經過1,582次的訓練後,梯度下降法得到的係數值與lm函數及封閉解的結果相同,訓練成功!
我們可以透過繪圖來了解機器學習的過程,首先需先繪製出誤差函數的等高線圖,再來將學習路徑標示在圖上。
# 計算不同截距項及係數項組合下的誤差函數值
plotData <- NULL
for(alpha in seq(-6000, 3000, 500)){
for(beta in seq(0, 24000, 500)){
# 計算均方誤差
yPred <- alpha+ beta %*% t(x)
mse <- sum((y-yPred)^2) / length(y)
# 紀錄資訊
plotData <- plotData %>% bind_rows(tibble(alpha, beta, mse))
}
}
# 繪製誤差函數的等高線圖形 並加入學習過程
ggplot(plotData, aes(x = beta, y = alpha, z = mse)) +
# 繪製等高線圖
stat_contour(aes(colour = ..level..), size = 1.3, bins = 20) +
# 修改等高線顏色
scale_colour_gradientn(colours = rainbow(20), name = "均方誤差") +
# 修改x軸名稱
xlab("beta") +
# 修改y軸名稱
ylab("alpha") +
# 標註梯度疊代每次的點位
geom_point(data = traningRecord,
mapping = aes(x = beta, y = alpha),
size = 1.3, shape = 21, fill = "white")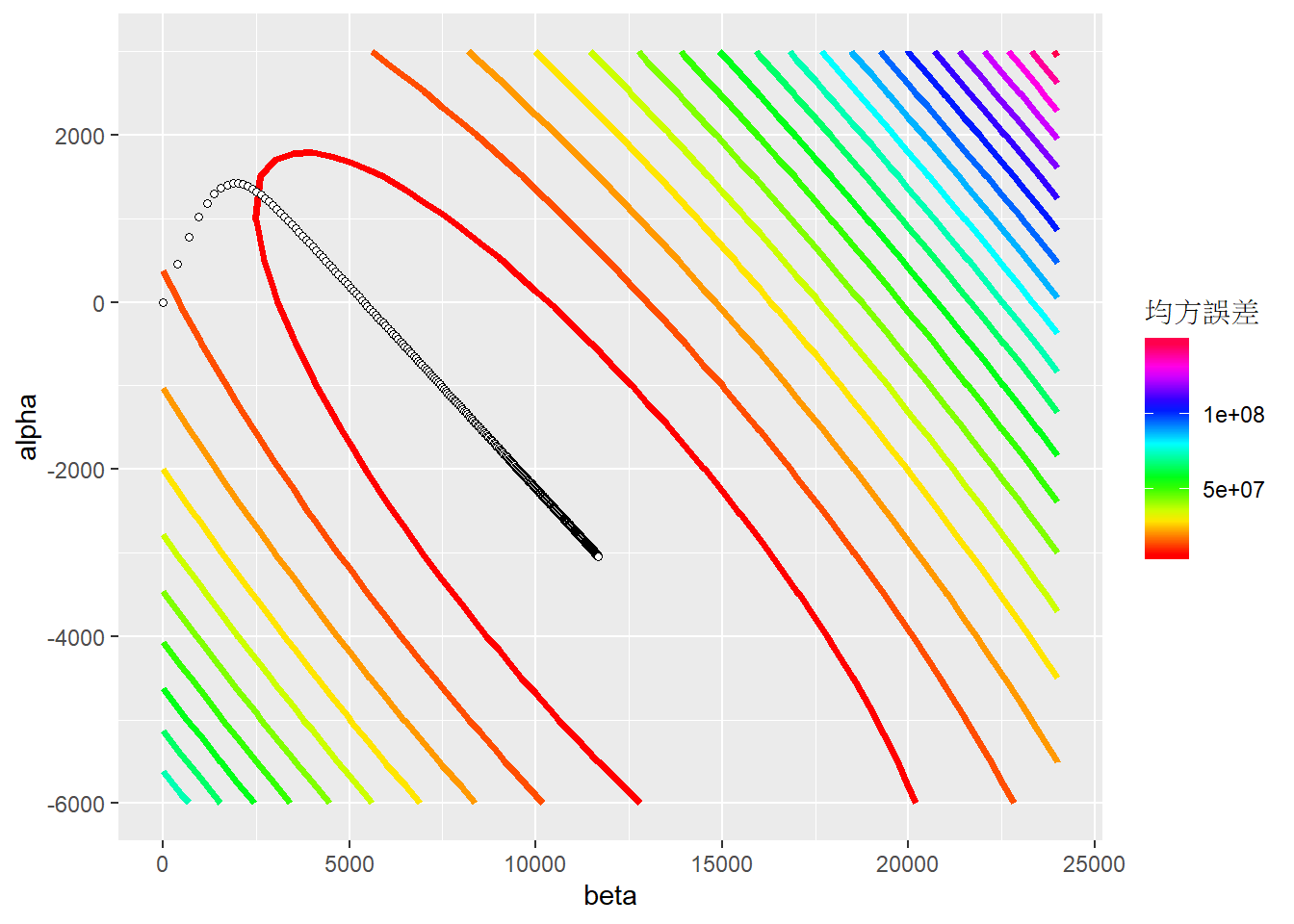
由圖可以看出,電腦從初始值(0,0)的地方,透過梯度下降法,一路收斂到均方誤差最小的地方。
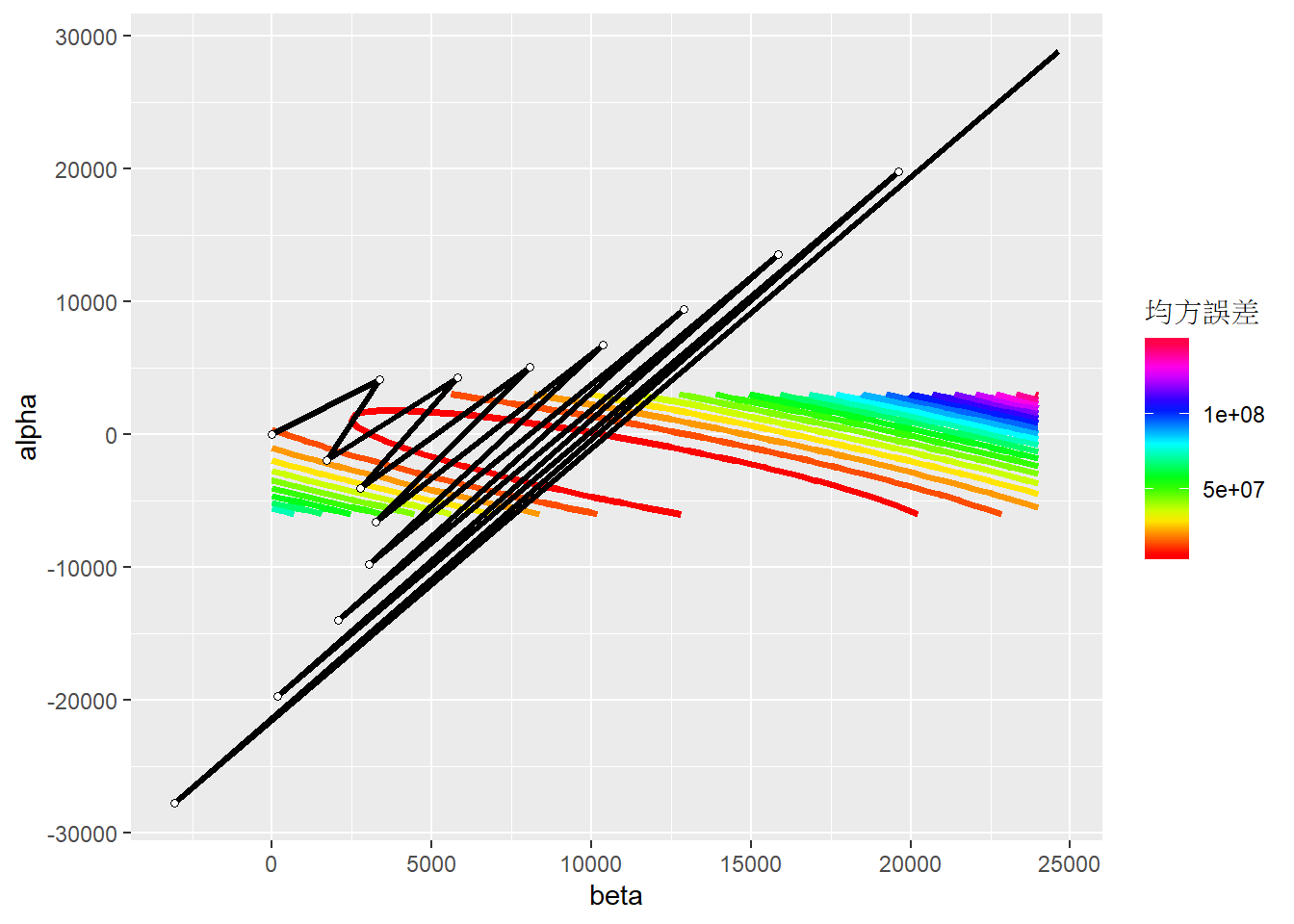
學習比率是梯度下降法中重要的參數,若設定太小,收斂速度會太慢。但若設定值太大,則會有梯度爆炸(Gradient explosion)的狀況出現,係數值會發散而無法收斂。

學習比率的設定依各個資料集的狀況而有所不同,在此範例中,若學習比率設定為0.9,就會發生梯度爆炸的狀況,如下圖:
comments powered by Disqus