上市股票Beta估計
前言
最近在幫老師製作教學講義的案例,要用資本資產定價模型(Capital Asset Pricing Model, CAPM),去估計2017年每支上市股票的\(\beta\)。這個問題在碩士班時就有用程式寫過,並沒有很難。但當時程式能力弱弱的,主要是用迴圈去一支一支計算。這次要寫這個程式有一些新的想法,之前看網路上的文章有用到apply家族可以一次估計多個模型的範例,因此透過這次的題目,可以把這個想法實作出來。
資本資產定價模型(CAPM)
資本資產定價模型(CAPM)是財務領域中的重要模型之一,主要用於解釋資本市場如何決定股票的報酬率。財金系的大二學生,在上財務管理或投資學時,一定會學到這個模型。此模型用一般無截距的最小平方法(Ordinary Least Squares, OLS)估計即可,模型如下:
\[E(R_i)-R_f=\beta (E(R_m)-R_f)\]
\(E(R_i)\):股票\(i\)的期望報酬率
\(E(R_i)-R_f\):股票\(i\)的市場風險溢酬
\(E(R_m)\):市場的期望報酬率
\(E(R_m)-R_f\):市場風險溢酬
\(R_f\):無風險利率
估計樣本的時間頻率一般會採用月頻,樣本數為近60個月。這個模型的重點是在看估計出來的\(\beta\),\(\beta\)是衡量這支股票報酬率與市場報酬率之間的連動性。
若\(\beta\)等於1,代表每當市場報酬率上升1%時,股票期望報酬也會跟著上升1%。
若\(\beta\)等於1.2,代表每當市場報酬率上升1%時,股票期望報酬會上升1.2%
若\(\beta\)等於0.5,代表每當市場報酬率上升1%時,股票期望報酬只會上升0.5%。
詳細的模型說明可參考維基百科。
資料來源
資料是從TEJ資料庫取得,我們以2017年12月為估計時點,需要60個月的樣本,因此資料期間為2013年1月至2017年12月。市場月報酬率以報酬指數計算得出,股票報酬率以調整後價格計算,無風險利率採用臺灣銀行一年期定存利率月化。
實作過程
資料整理的部份此處略過,主要是透過tidyverse套件來整理資料,並確保每支股票在2013年1月至2017年12月之間,共有60筆完整樣本,若沒有則會被踢除。資料整理完後,欄位如下圖所示:
library(tidyverse)# 讀取資料
load("./stock-beta/data.Rdata")# 呈現資料前10筆內容
head(data,10) ## # A tibble: 10 x 5
## code name yearMonth monthRetDiffRf mktRetDiffRf
## <chr> <chr> <chr> <dbl> <dbl>
## 1 1101 台泥 201301 0.0219 0.00798
## 2 1101 台泥 201302 -0.0510 0.00422
## 3 1101 台泥 201303 -0.0357 -0.00690
## 4 1101 台泥 201304 0.0429 0.0235
## 5 1101 台泥 201305 0.0235 0.0145
## 6 1101 台泥 201306 -0.0402 -0.0170
## 7 1101 台泥 201307 0.0408 0.0263
## 8 1101 台泥 201308 0.0663 0.00128
## 9 1101 台泥 201309 0.0837 0.0167
## 10 1101 台泥 201310 0.0240 0.0310欄位依序為股票代碼(code)、股票名稱(name)、年月(yearMonth)、股票風險溢酬(monthRetDiffRef)及市場風險溢酬(mktRetDiffRf)。我們對資料做一些簡單的確認:
# 完整期間(60個月)的股票家數
length(unique(data$code)) ## [1] 814# 資料起始月份
min(data$yearMonth) ## [1] "201301"# 資料結束月份
max(data$yearMonth) ## [1] "201712"接下來開始估計每支股票的\(\beta\),先把CAPM模型部份包成函數。此處因為只需要輸出一個\(\beta\),所以只要用sapply()即可,程式碼如下:
library(tidyverse)
stockList <- unique(data$code) # 股票清單
# CAPM自製函數
CapmModel <- function(ix){
# 讀取股票資料
iData <- data %>% filter(code==ix)
# 無截距模型估計
model <- lm(formula= monthRetDiffRf ~ 0 + mktRetDiffRf, data= iData)
# 取出Beta
beta <- model$coefficients
return(as.numeric(beta))
}
# 啟動計時器
ptm <- proc.time()
# 估計模型
result <- sapply(stockList, CapmModel)
# 結束計時器
ptm <- proc.time() - ptm
# 整理資料表
result <- tibble(code=stockList, beta=result)# 呈現估計結果資料前10筆內容
head(result, 10) ## # A tibble: 10 x 2
## code beta
## <chr> <dbl>
## 1 1101 1.14
## 2 1102 0.837
## 3 1103 1.03
## 4 1104 1.13
## 5 1108 0.538
## 6 1109 0.784
## 7 1110 0.575
## 8 1201 0.631
## 9 1203 0.526
## 10 1210 0.972# 執行時間
ptm## user system elapsed
## 1.12 0.13 1.25這邊有一個地方可以提速,就是可以不用使用lm()函數,直接套公式解出\(\beta\)。因為lm函數執行時會同時紀錄其他迴歸的資訊(例如\(R^2\)等),是我們不需要的,所以如果套公式解,就可以少算很多東西。無截距最小平方模型的\(\beta\)估計式(參考)為:
\[\beta=(X^TX)^{-1}X^TY\]
# CAPM自製函數
CapmModel <- function(ix){
# 讀取股票資料
iData <- data %>% filter(code==ix)
# 公式解Beta
x <- iData$mktRetDiffRf
y <- iData$monthRetDiffRf
beta <- (solve(x%*%x)%*%x%*%y) %>% as.vector()
return(as.numeric(beta))
}
# 啟動計時器
ptm <- proc.time()
# 估計模型
result <- sapply(stockList, CapmModel)
# 結束計時器
ptm <- proc.time() - ptm
# 整理資料表
result <- tibble(code=stockList, beta=result)# 呈現估計結果資料前10筆內容
head(result, 10) ## # A tibble: 10 x 2
## code beta
## <chr> <dbl>
## 1 1101 1.14
## 2 1102 0.837
## 3 1103 1.03
## 4 1104 1.13
## 5 1108 0.538
## 6 1109 0.784
## 7 1110 0.575
## 8 1201 0.631
## 9 1203 0.526
## 10 1210 0.972# 執行時間
ptm## user system elapsed
## 0.61 0.11 0.72透過程式的執行時間,可以看出直接輸入公式解\(\beta\)比使用lm()函數快上許多。
2017年12月每支股票的\(\beta\)估計完後,可以來做一些簡單的分析。
# 併入股票名稱
result <- result %>%
left_join(distinct(data, code, name), by=c("code"="code")) %>%
select(code, name, beta)
# Beta前10名股票
result %>% arrange(desc(beta)) %>% filter(row_number()<=10) ## # A tibble: 10 x 3
## code name beta
## <chr> <chr> <dbl>
## 1 1475 本盟 3.34
## 2 2439 美律 2.91
## 3 2305 全友 2.67
## 4 6116 彩晶 2.67
## 5 4739 康普 2.66
## 6 8261 富鼎 2.66
## 7 2491 吉祥全 2.52
## 8 2364 倫飛 2.51
## 9 2337 旺宏 2.46
## 10 6243 迅杰 2.45# Beta後10名股票
result %>% arrange(beta) %>% filter(row_number()<=10) ## # A tibble: 10 x 3
## code name beta
## <chr> <chr> <dbl>
## 1 910708 恒大健-DR -1.35
## 2 2496 卓越 -0.706
## 3 2722 夏都 -0.331
## 4 911608 明輝-DR -0.206
## 5 1436 華友聯 -0.0837
## 6 4119 旭富 -0.0433
## 7 910482 聖馬丁-DR -0.0395
## 8 9929 秋雨 -0.0394
## 9 8101 華冠 -0.0268
## 10 1220 台榮 0.0342# 繪製Beta的分配圖
ggplot(result, aes(x=beta)) + geom_histogram()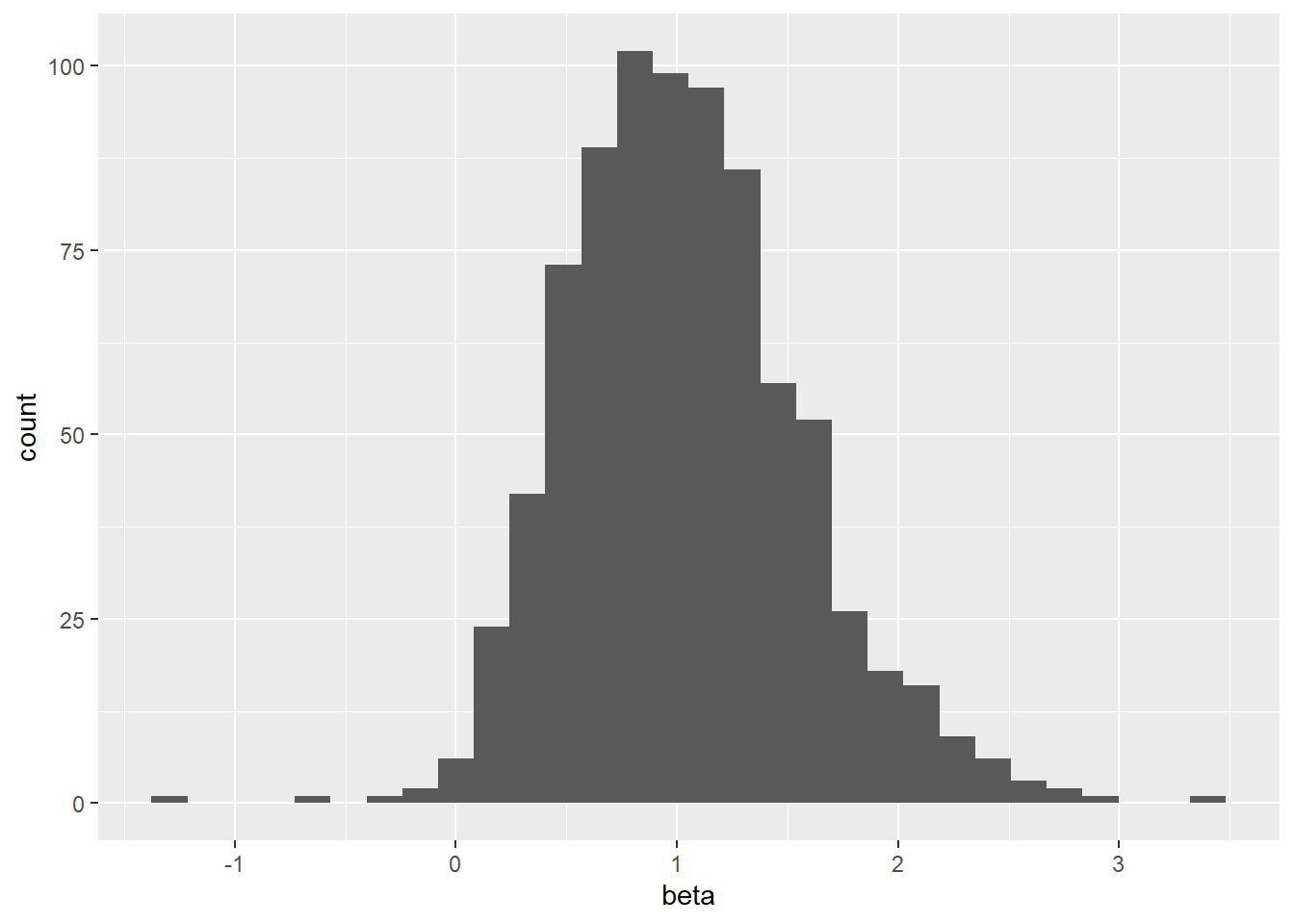
可以繪製單一股票估計的CAPM模型迴歸線,例如2330台積電。
plotCode <- 2330
iData <- data %>% filter(code==plotCode)
ggplot(iData, aes(x=mktRetDiffRf, y=monthRetDiffRf)) +
geom_point() +
geom_smooth(method = "lm", formula = y ~ 0 + x, se = F) +
labs(title=paste0(plotCode," CAPM模型"), x ="市場風險溢酬", y = "股票風險溢酬")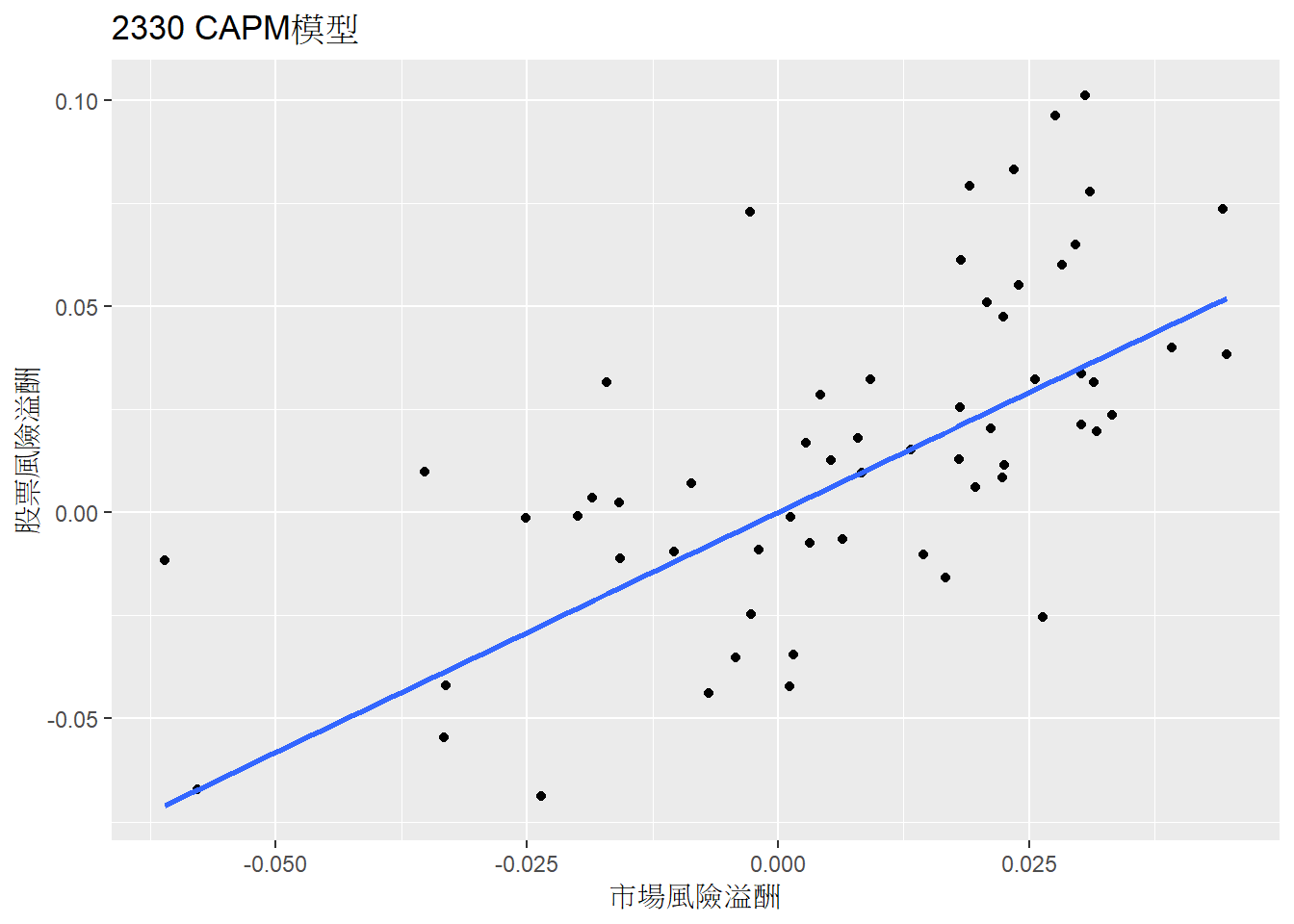
也可以同時繪製多檔股票進行比較,這邊選擇2330台積電、2412中華電及3008大立光。
plotCode <- c(2330, 2412, 3008)
iData <- data %>% filter(code %in% plotCode)
ggplot(iData, aes(x=mktRetDiffRf, y=monthRetDiffRf, colour=code)) +
geom_point() +
geom_smooth(method = "lm", formula = y ~ 0 + x, se = F) +
labs(title=paste0("CAPM模型比較"), x ="市場風險溢酬", y = "股票風險溢酬")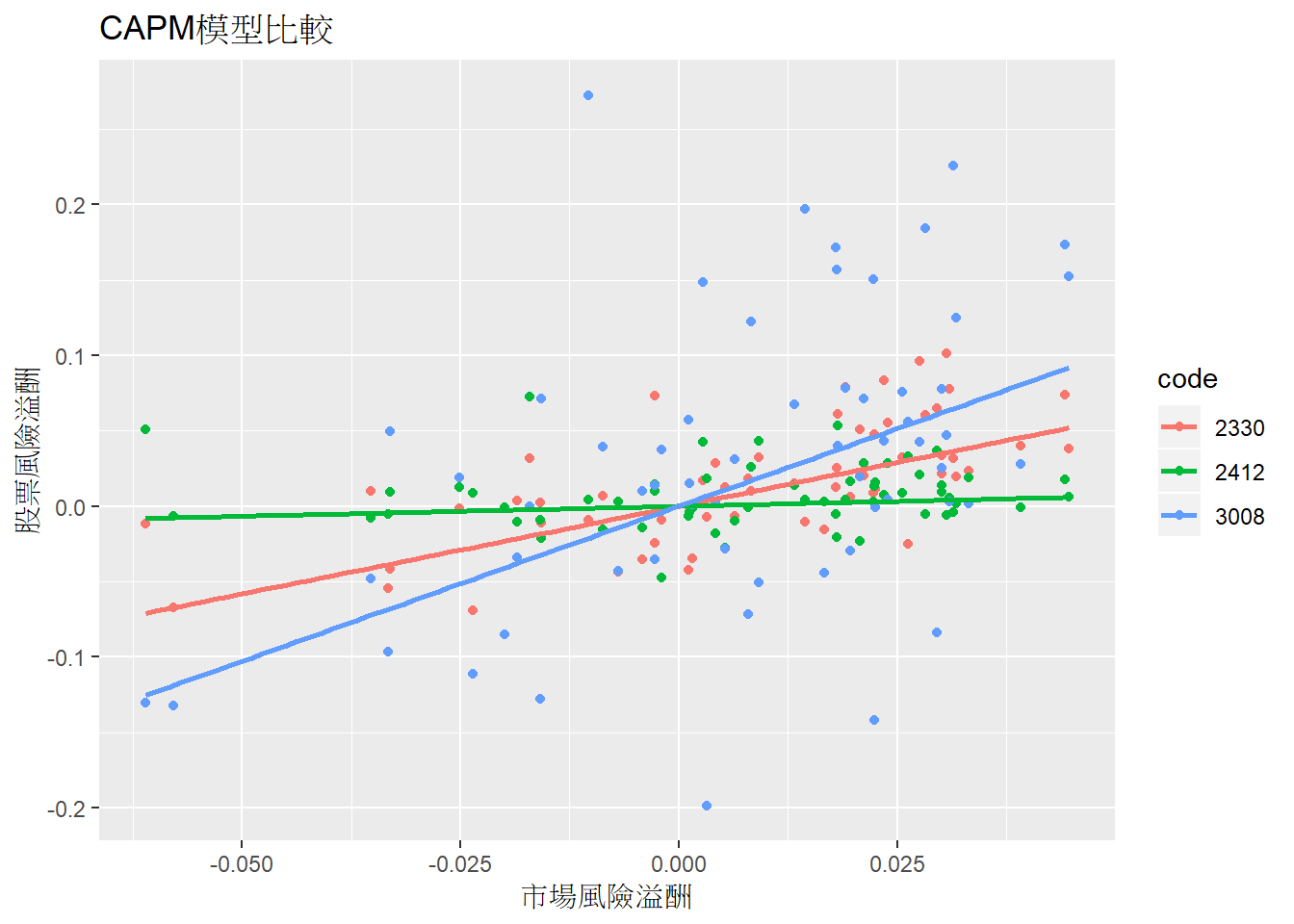
從上圖可以看出,2412中華電信的迴歸線斜率(也就是\(\beta\))接近0,股價不會隨著市場走勢有所變動。\(\beta\)本身即是反映一檔股票背後的市場風險。在市場走多頭時,投資人可以勇敢投資高\(\beta\)股票,讓自己的報酬率比市場報酬率還高;市場走空頭時,則可轉為投資低\(\beta\)股票,抵擋市場不景氣時帶來的影響。
comments powered by Disqus